Is MOT piecewise linear?
How linearly do people walk?

MOT is one of the most widely used evaluation datasets for object tracking. MOT17 is now 6+ years old, and while the benchmark has newer versions like MOT20, even the older MOT17 is also still used as a key SOTA benchmark:
Papers with Code - MOT17 Benchmark (Multi-Object Tracking)
And yet the ground truth is piecewise linear. Sort of.
Note: You can check out the code for this project here: https://github.com/smrfeld/mot-linearity.
Taking a look at MOT17
Let’s grab a few of the ground truth (GT) trajectories from the MOT17 dataset, and plot them. In the following figure, we show the initial and final bounding boxes, as well as the trajectory of the top-left and bottom-right points.
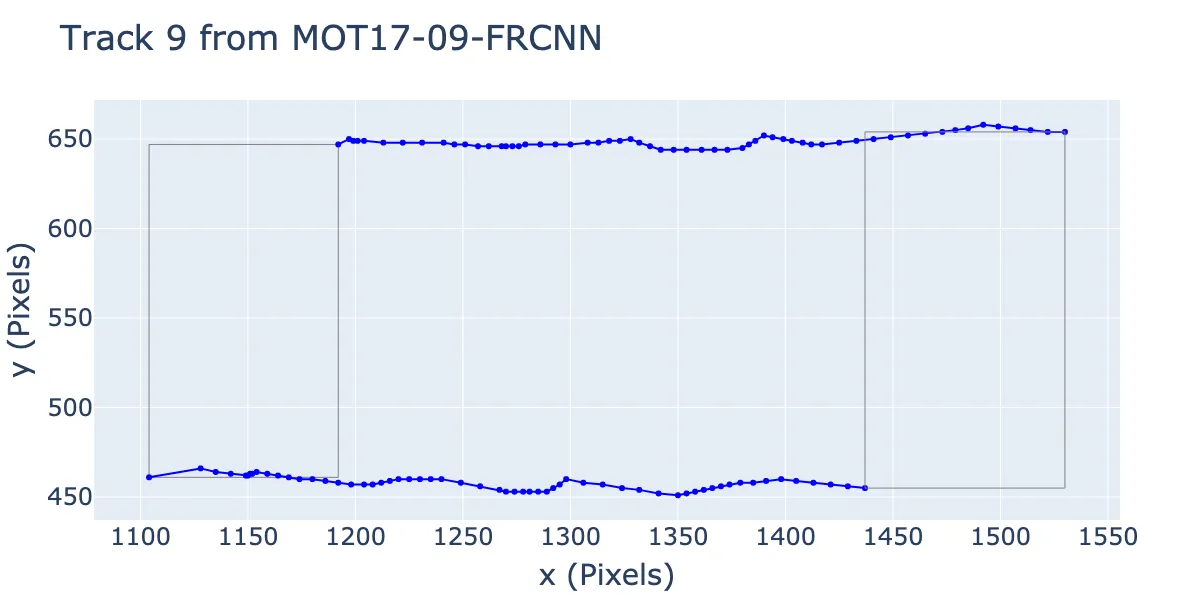 A single track from MOT17. The start and end bounding boxes are in gray, and all intermediate points for the bottom left and top right corners shown. Note that in an image, the y axis would be inverted (not important here).
A single track from MOT17. The start and end bounding boxes are in gray, and all intermediate points for the bottom left and top right corners shown. Note that in an image, the y axis would be inverted (not important here).
There are a lot of linear pieces here! For example between x=[1300,1350], or x=[1400,1440]. Is it an outlier?
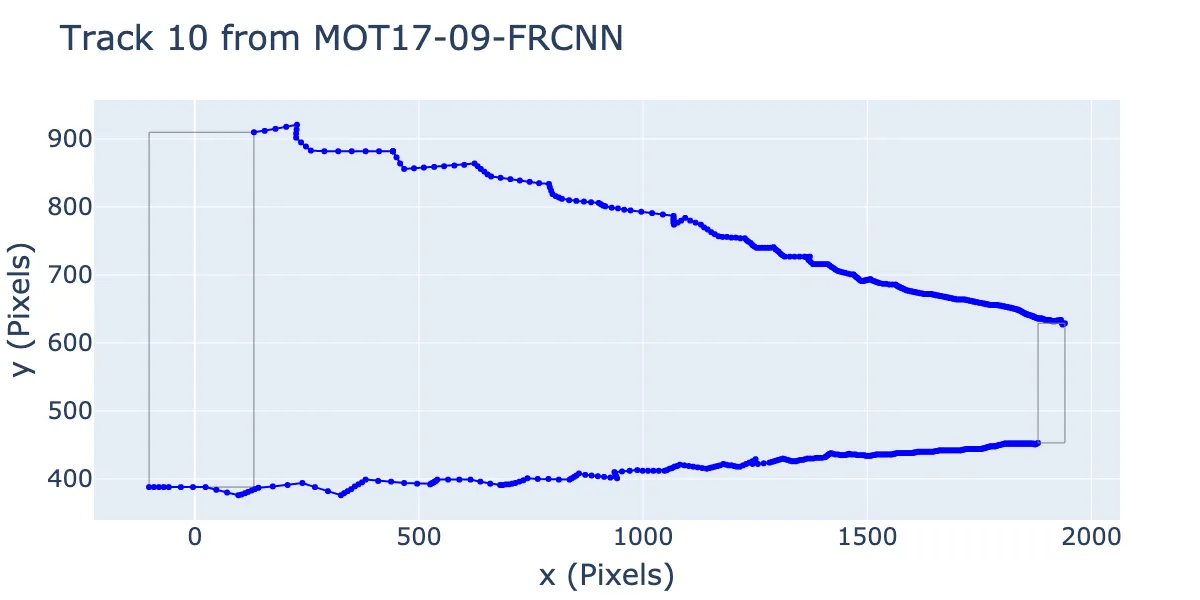 Another trajectory — the end doesn’t look as linear, but the beginning has clear linear segments.
Another trajectory — the end doesn’t look as linear, but the beginning has clear linear segments.
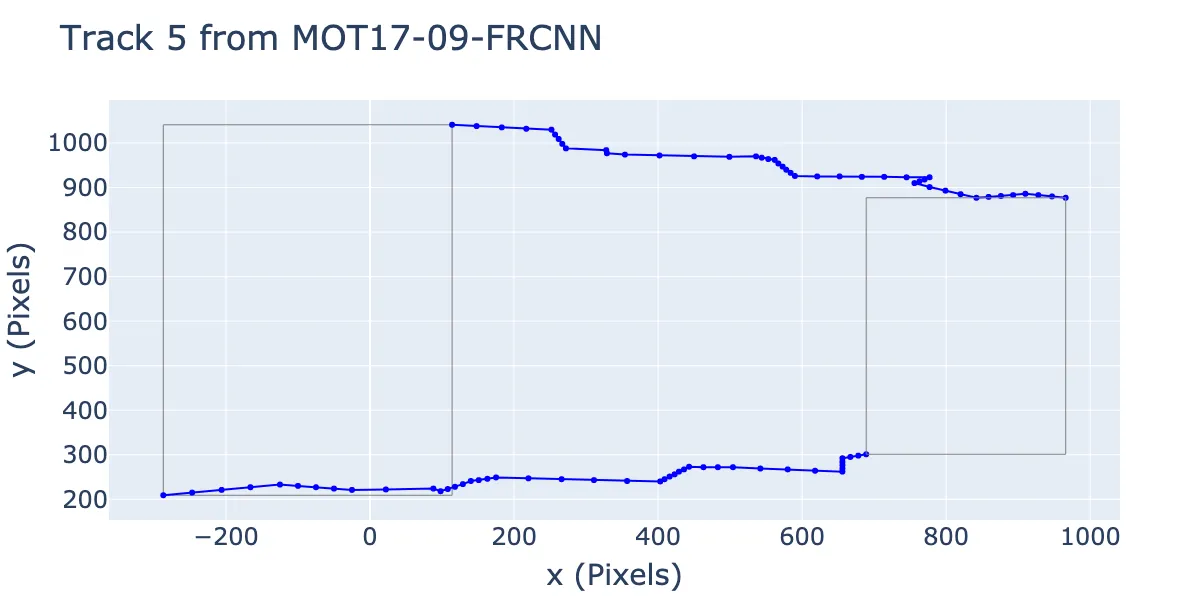 A final piecewise linear trajectory.
A final piecewise linear trajectory.
It doesn’t look like this is outliers — it looks like the trajectories are at least somewhat piecewise linear.
But just how linear is linear?
Let’s find out!
But we need a way to measure linearity. We have a time series consisting of points that we think are piecewise linear. How can we tell if a section is a linear one?
Between two points, there is only one line, so we need to look at 3 points. Between three points, there are two line segments connecting the three points. If the three points lie in a line, the slopes of the two line segments will be the same.
We can therefore scan through the time series in triplets, and check if three points lie in a line by checking if the difference in slopes differs by less than some tolerance tol. If the condition is met, we mark the three points as belonging to a linear segment.
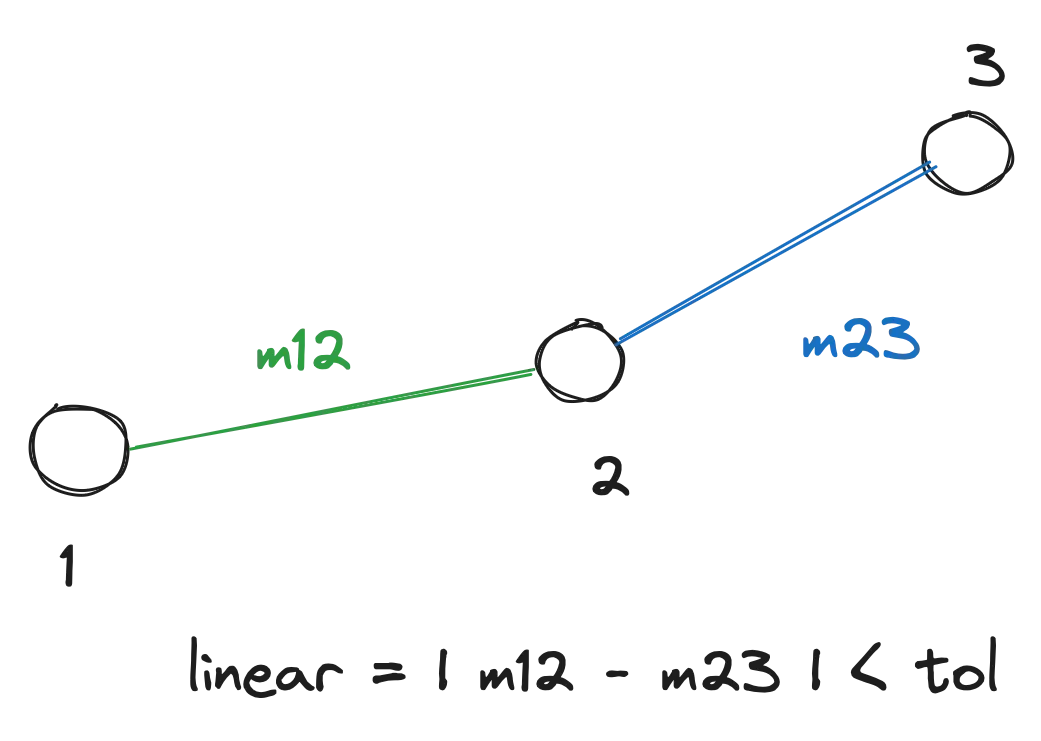 Scanning through the time series in triplets, we can check if three points lie in a line up to tolerance tol. If the condition is met, we mark the three points as belonging to a linear segment.
Scanning through the time series in triplets, we can check if three points lie in a line up to tolerance tol. If the condition is met, we mark the three points as belonging to a linear segment.
In the analysis, we also exclude any triplets of points where all 3 points are the same, i.e. the person is standing still, since this doesn’t really count as moving linearly.
Finally, since we are dealing with bounding boxes instead of points, we will look at both the bottom left corner and the top right corner of the box. Only of both triplets are linear, then we mark the motion of the box as linear. If either triplet is not linear, then we discount it. Note that while both corners have to move linearly, we don’t require them to move linearly with the same slope — this allows e.g. the bounding box to resize as the person walks closer to the camera.
Limitation: since we are only “greedily” considering three points at a time, it’s possible that small errors could add up over many points, such that the line segment ends up falsely being marked as linear when it’s not. Nothing is perfect! Looking at the plots below, we can see this is not likely the case here.
Here is the result for the previous track, where we mark the linear line segments we identified with red lines. The tolerance used is 0, i.e. we require the points to perfectly lie in a line.
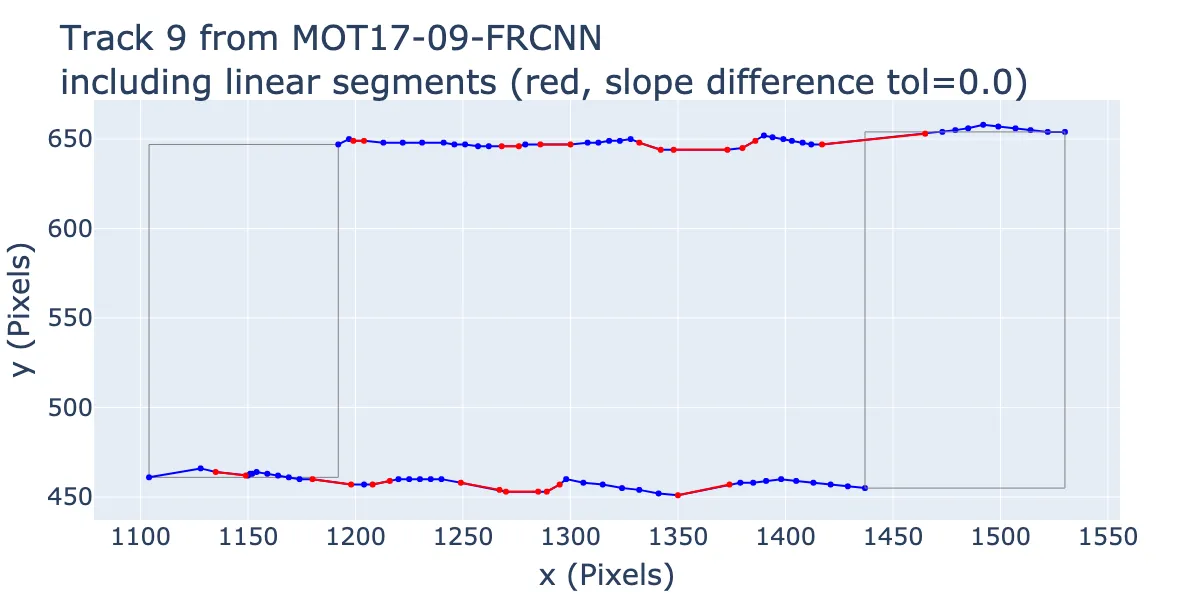 Linear segments identified from the piecewise linear analysis. Blue points indicate the points in the original trajectory. Red lines indicate the linear segments. The tolerance used is 0, i.e. the points must perfectly lie in a line.
Linear segments identified from the piecewise linear analysis. Blue points indicate the points in the original trajectory. Red lines indicate the linear segments. The tolerance used is 0, i.e. the points must perfectly lie in a line.
Here are some side-by-side comparisons:
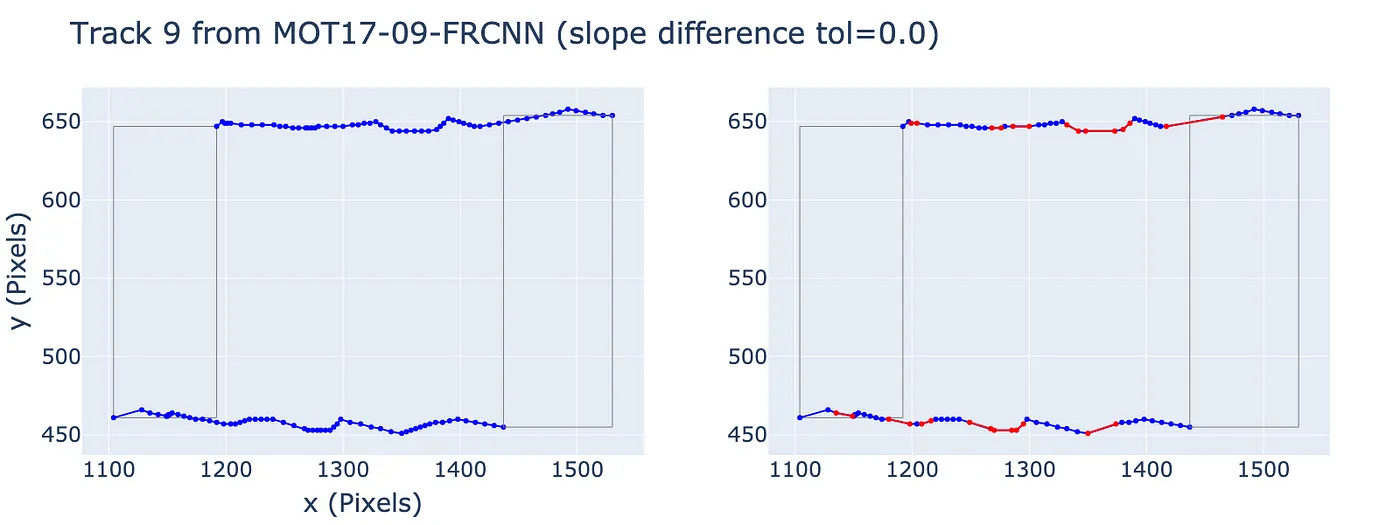 Side-by-side comparison. Left: original trajectory. Right: piecewise linear segments with slope difference tolerance = 0.
Side-by-side comparison. Left: original trajectory. Right: piecewise linear segments with slope difference tolerance = 0.
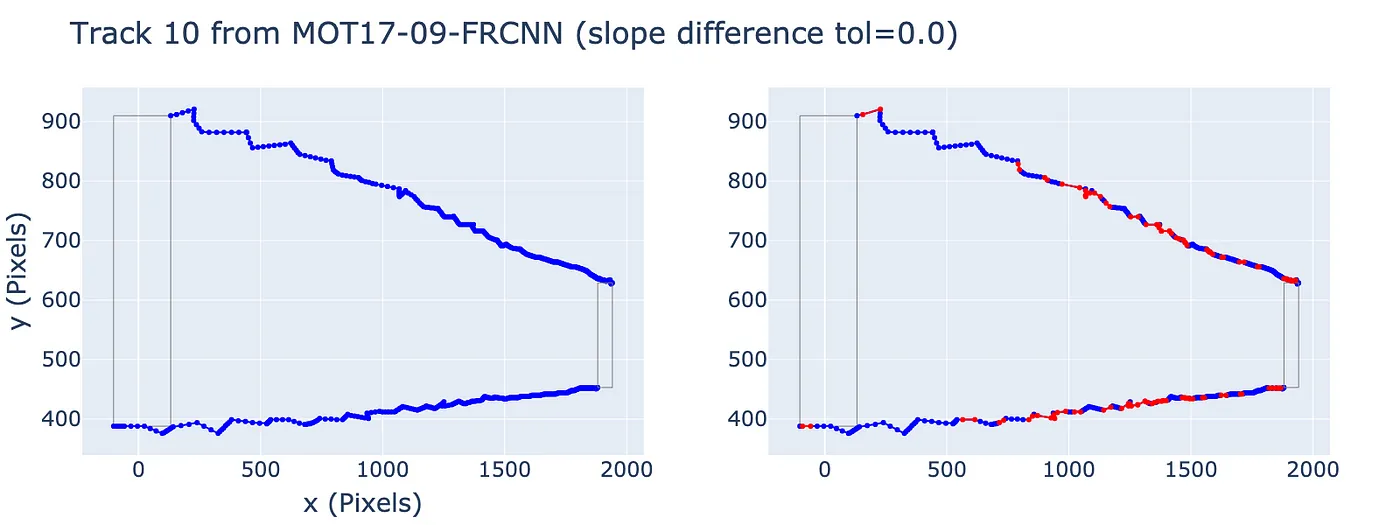 Side-by-side comparison. Left: original trajectory. Right: piecewise linear segments with slope difference tolerance = 0.
Side-by-side comparison. Left: original trajectory. Right: piecewise linear segments with slope difference tolerance = 0.
This did OK, but we still find that the there are many segments that look linear, but are not perfectly linear. Measured across all the trajectories in the dataset, we find at tolerance = 0, about 26% of the points belong to linear segments (of at least 3 points in length).
What if we increase the tolerance?
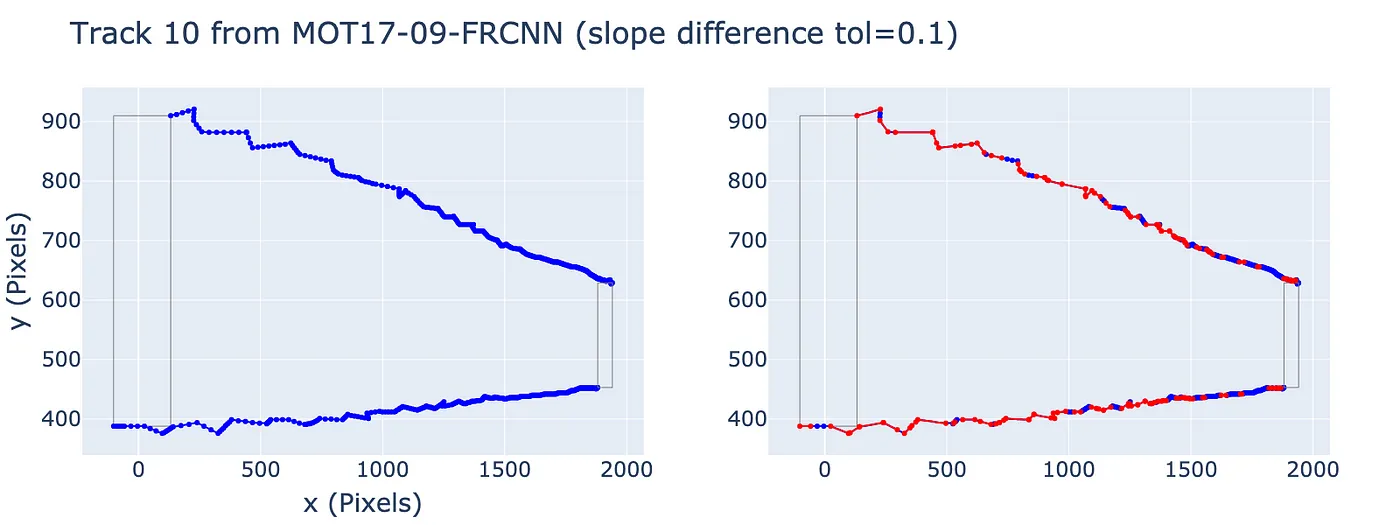 Side-by-side comparison with tolerance=0.1 for the slope difference. Much of the trajectory is identified as consisting of piecewise linear segments.
Side-by-side comparison with tolerance=0.1 for the slope difference. Much of the trajectory is identified as consisting of piecewise linear segments.
At tolerance 0.1, we find that much of the trajectory is made of piecewise linear segments. Measured across all trajectories, we get to about 39% of the points in the trajectories belonging to linear segments (of at least 3 points in length).
How long are these linear pieces?
Are most linear segments really short? The minimum length of a linear segment is just three points. Does it dominate the distribution? Let’s look at a histogram:
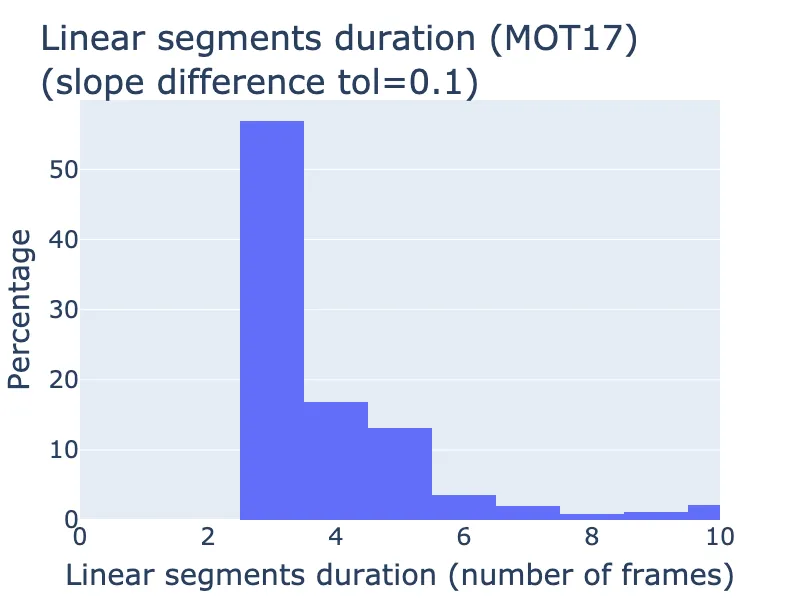 Duration of linear segments in MOT17. The distribution is certainly peaked at the minimum length of 3 frames, with 50% of the linear segments being just 3 frames long, but also with a long tail for longer segments.
Duration of linear segments in MOT17. The distribution is certainly peaked at the minimum length of 3 frames, with 50% of the linear segments being just 3 frames long, but also with a long tail for longer segments.
The duration is certainly peaked at the minimum length of 3 frames, with 50% of the linear segments being just 3 frames long, but there is also a long tail. You could argue that such short segments should not be counted in the analysis, but they’re still significant (see random walks below).
Tolerance tolerance tolerance
Let’s summarize how the tolerance affects the percentage of the points in the trajectory that belong to linear segments:
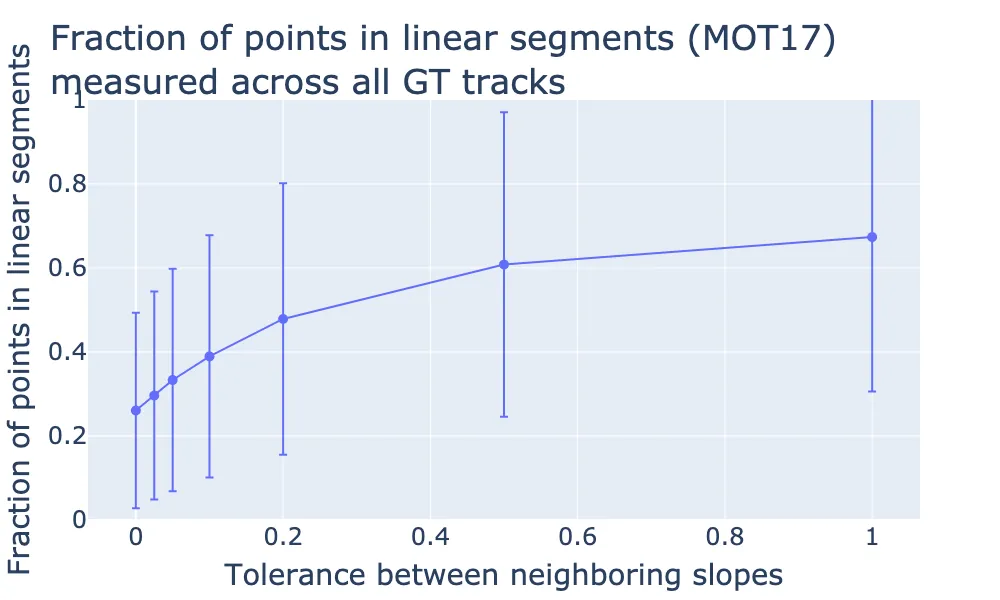 How the tolerance affects the percentage of points that belong to linear segments. Looking at tolerance = 0 where the points have to perfectly lie in a line, we see about 26% of the points belong to linear segments. If we increase the tolerance significantly, we can get over 60% of the points to be approximately linear. Error bars come from computing the fraction for different trajectories (different person tracks, across all videos in the dataset).
How the tolerance affects the percentage of points that belong to linear segments. Looking at tolerance = 0 where the points have to perfectly lie in a line, we see about 26% of the points belong to linear segments. If we increase the tolerance significantly, we can get over 60% of the points to be approximately linear. Error bars come from computing the fraction for different trajectories (different person tracks, across all videos in the dataset).
Looking at tolerance = 0.1 where the points have to perfectly lie in a line, we see about 39% of the points belong to linear segments (of at least 3 points in length). If we increase the tolerance significantly, we can get over 60% of the points to be approximately linear.
I don’t like hyperparameters
Me too! What is this tolerance parameter thing? Let’s take one more deeper look at the data — why might the points not perfectly lie in a line?
The points in the original trajectories are integer values. We can assume that the annotators draw bounding boxes in some UX, but since the values are rounded to integers, we could be off by as much as 0.5 pixels in either x or y.
With that in mind, let’s revisit the three points that we are using to test for linearity. If we consider perturbing the three points by some small magnitude p, we can derive the minimum and maximum slopes of the two segments. This gives a range of slopes M = [m_min,m_max] for each line segments. If the two ranges overlap, then we can say that the points lie in a line.
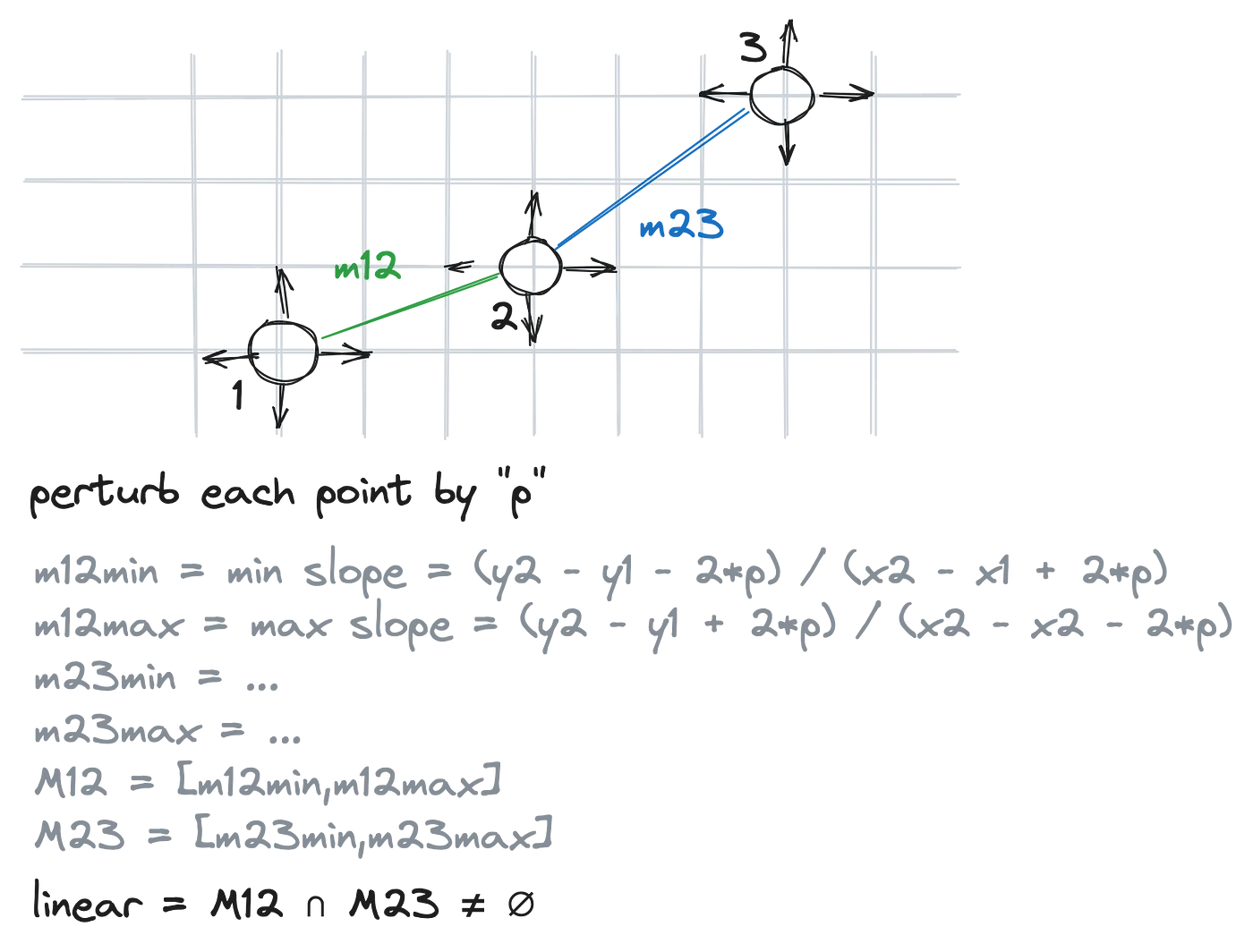 A different way of assessing linearity. Consider perturbing each point by a small
A different way of assessing linearity. Consider perturbing each point by a small p. From this we can write the minimum and maximum slope of each line segment. This gives a range of slopes for each of the two segments M12 and M23. If the two ranges overlap, we can say that the points are in a line.
What value should we use for the perturbation magnitude? A natural choice is p=0.5, since we discussed above that this is the possible error in the pixel coordinates.
With this new algorithm, we no longer need any tolerance hyperparameters. We can use it the same way as before, sliding along the trajectory and considering 3 points at a time to determine linearity.
From this approach, 39% of the points from all the ground truth trajectories in the MOT17 dataset are identified with linear segments (of at least 3 points in length).
MOT20
Repeating the analysis on the MOT20 dataset gives a similar result of 42% of the points from all the ground truth trajectories associated with linear segments (of at least 3 points in length), where the perturbations were p=0.5. Or, using the tolerance analysis:
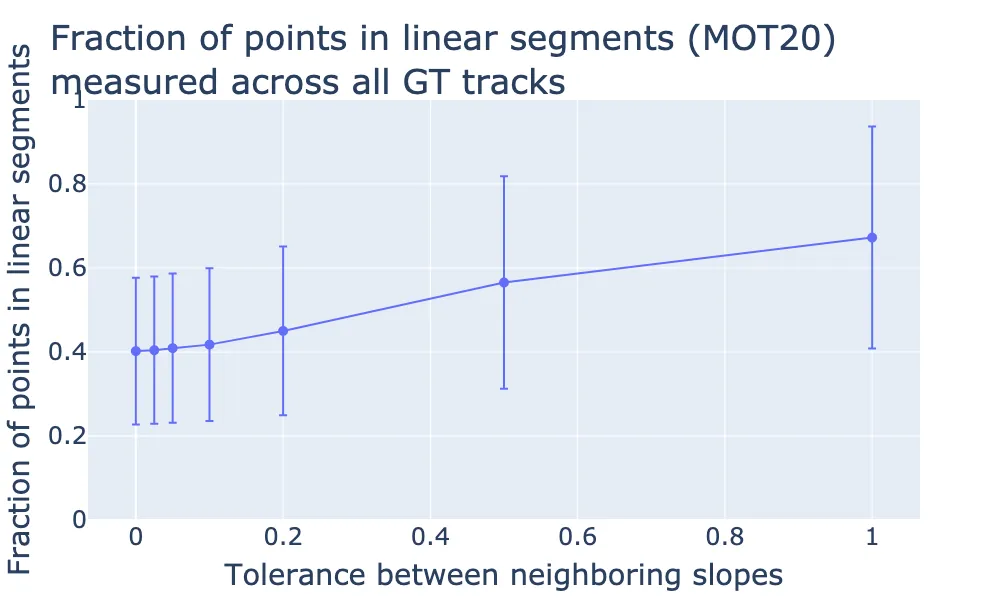 Analysis using tolerance based method for MOT20.
Analysis using tolerance based method for MOT20.
What if it’s random?
We need a baseline to test against. Let’s consider a random walk. We can measure the displacements of the bounding boxes (top left and bottom right corners) in the ground truth MOT 17 data:
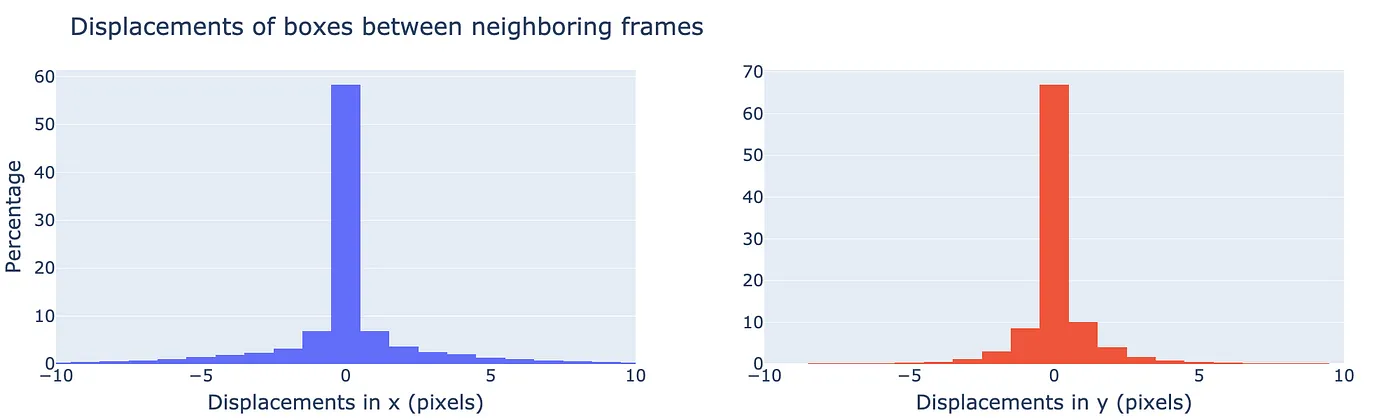 Displacements in the ground truth MOT17 data. Most of the steps involve no displacement.
Displacements in the ground truth MOT17 data. Most of the steps involve no displacement.
Next, we can simulate some random walks with the same distribution of steps, and repeat the analysis. Here is one such example:
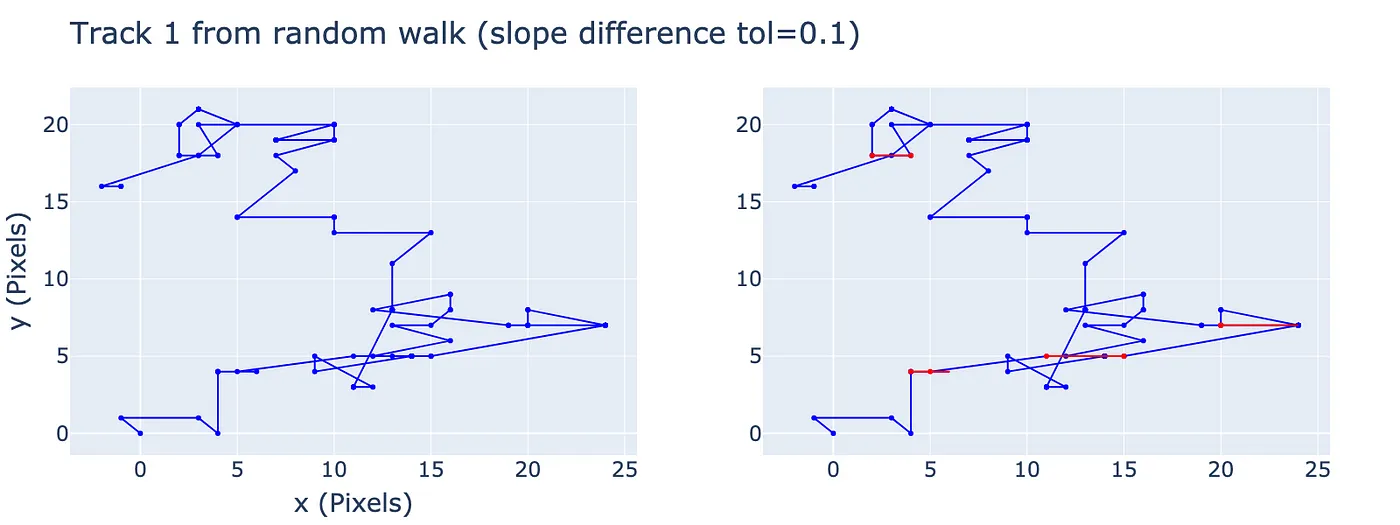 Random walk generated from the same distribution of coordinate displacements. Left: the random walk. Right: the piecewise linear pieces, identified with tolerance=0.1 in red. Note that triplets of points where (pt1==pt2==pt3) where the trajectory did not change are not considered (as was done above, where the bounding box does not change).
Random walk generated from the same distribution of coordinate displacements. Left: the random walk. Right: the piecewise linear pieces, identified with tolerance=0.1 in red. Note that triplets of points where (pt1==pt2==pt3) where the trajectory did not change are not considered (as was done above, where the bounding box does not change).
Here is another one:
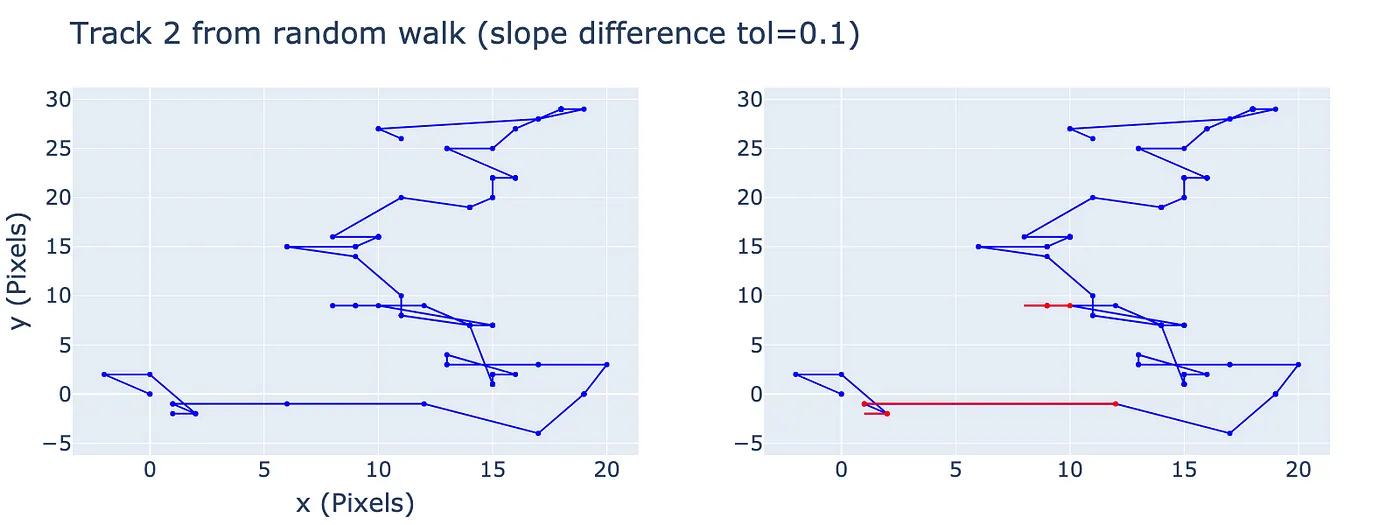 Another random walk.
Another random walk.
It already looks less piecewise linear. Repeating the analysis from above, we find that only 8% of points belong to linear segments.
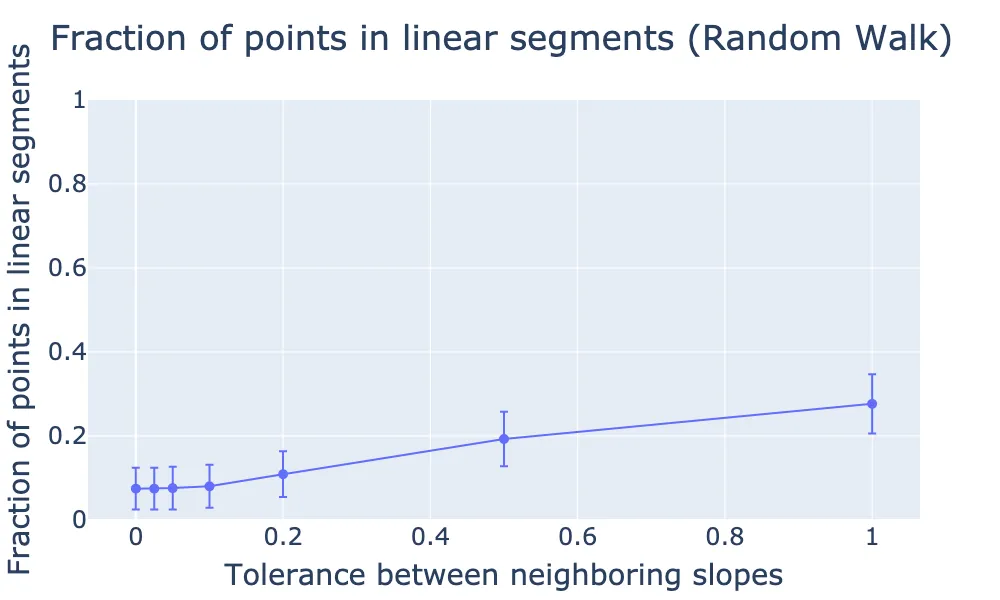 Fraction of points belonging to linear segments as a function of the slop tolerance. Using this as a measure of how piecewise linear the trajectories are, we find the random walk is much less piecewise linear (unsurprising).
Fraction of points belonging to linear segments as a function of the slop tolerance. Using this as a measure of how piecewise linear the trajectories are, we find the random walk is much less piecewise linear (unsurprising).
For the random walks here, we only considered trajectories of (x,y) points, instead of trajectories of bounding boxes (x0,y0,x1,y1). In the bounding box linearity analysis we performed above, both the corner points have to move linearly for us to consider the trajectory as linear. So a random walk of a bounding box (where both corners undergo a random walk) is even less linear (in reality, we would expect the width and height of the bounding boxes to be relatively consistent frame-to-frame, we only the position should undergo a random walk). So clearly, MOT is much more linear than a random walk.
Final thoughts
Let’ summarize: we found that nearly 40% of the points in the ground truth of the MOT17 dataset belong to linear segments. MOT20 shows similar behavior.
But enough data analysis. We didn’t really answer why the motions look piecewise linear. There are two possible answers:
-
Annotators used an annotation tool that produces piecewise linear motion. Annotating bounding boxes is time consuming, and some labeling interfaces let annotators simply draw a starting bounding box and an ending bounding box several frames later, and the interpolate linearly in between the two. Clearly, it’s important to understand how our data is labeled.
-
People really do walk somewhat linearly, unless they’re demonstrating Brownian motion for us by stumbling home from the pub.
Thanks for reading and diving into some real-world data with me.
Appendix
- What exact MOT17 data? For this analysis we used the train split and the gt files:
MOT17–02 MOT17–04 MOT17–05 MOT17–09 MOT17–10 MOT17–11 MOT17–13 - What exact MOT20 data? We used the train split and the gt files:
MOT20-01 MOT20-02 MOT20-03 MOT20-05 - Where’s your code? https://github.com/smrfeld/mot-linearity
Contents
Oliver K. Ernst
October 22, 2023
