arXiv: arXiv:2109.05053

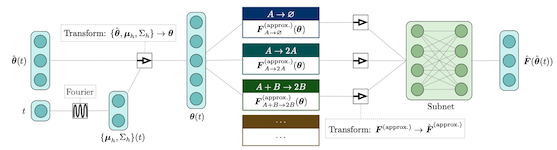
We present a machine learning method for model reduction which incorporates domain-specific physics through candidate functions. Our method estimates an effective probability distribution and differential equation model from stochastic simulations of a reaction network. The close connection between reduced and fine scale descriptions allows approximations derived from the master equation to be introduced into the learning problem. This representation is shown to improve generalization and allows a large reduction in network size for a classic model of inositol trisphosphate (IP3) dependent calcium oscillations in non-excitable cells.

arXiv: arXiv:1905.12122

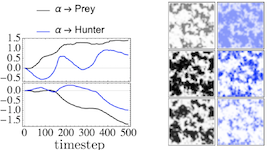
The moments of spatial probabilistic systems are often given by an infinite hierarchy of coupled differential equations. Moment closure methods are used to approximate a subset of low order moments by terminating the hierarchy at some order and replacing higher order terms with functions of lower order ones. For a given system, it is not known beforehand which closure approximation is optimal, i.e. which higher order terms are relevant in the current regime. Further, the generalization of such approximations is typically poor, as higher order corrections may become relevant over long timescales. We have developed a method to learn moment closure approximations directly from data using dynamic Boltzmann distributions (DBDs). The dynamics of the distribution are parameterized using basis functions from finite element methods, such that the approach can be applied without knowing the true dynamics of the system under consideration. We use the hierarchical architecture of deep Boltzmann machines (DBMs) with multinomial latent variables to learn closure approximations for progressively higher order spatial correlations. The learning algorithm uses a centering transformation, allowing the dynamic DBM to be trained without the need for pre-training. We demonstrate the method for a Lotka-Volterra system on a lattice, a typical example in spatial chemical reaction networks. The approach can be applied broadly to learn deep generative models in applications where infinite systems of differential equations arise.

arXiv: arXiv:1808.08630

Publication: Phys Rev E. 99, 063315 (2019)

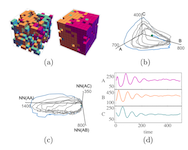
Many physical systems are described by probability distributions that evolve in both time and space. Modeling these systems is often challenging to due large state space and analytically intractable or computationally expensive dynamics. To address these problems, we study a machine learning approach to model reduction based on the Boltzmann machine. Given the form of the reduced model Boltzmann distribution, we introduce an autonomous differential equation system for the interactions appearing in the energy function. The reduced model can treat systems in continuous space (described by continuous random variables), for which we formulate a variational learning problem using the adjoint method for the right hand sides of the differential equations. This approach allows a physical model for the reduced system to be enforced by a suitable parameterization of the differential equations. In this work, the parameterization we employ uses the basis functions from finite element methods, which can be used to model any physical system. One application domain for such physics-informed learning algorithms is to modeling reaction-diffusion systems. We study a lattice version of the R{ö}ssler chaotic oscillator, which illustrates the accuracy of the moment closure approximation made by the method, and its dimensionality reduction power.

arXiv: arXiv:1803.01063

Publication: J. Chem. Phys 149 034107

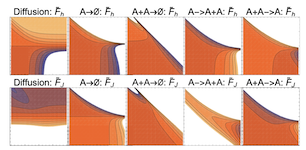
Finding reduced models of spatially-distributed chemical reaction networks requires an estimation of which effective dynamics are relevant. We propose a machine learning approach to this coarse graining problem, where a maximum entropy approximation is constructed that evolves slowly in time. The dynamical model governing the approximation is expressed as a functional, allowing a general treatment of spatial interactions. In contrast to typical machine learning approaches which estimate the interaction parameters of a graphical model, we derive Boltzmann-machine like learning algorithms to estimate directly the functionals dictating the time evolution of these parameters. By incorporating analytic solutions from simple reaction motifs, an efficient simulation method is demonstrated for systems ranging from toy problems to basic biologically relevant networks. The broadly applicable nature of our approach to learning spatial dynamics suggests promising applications to multiscale methods for spatial networks, as well as to further problems in machine learning.

Publication: Inverse Problems 30 114019

This article addresses the problem of compensating for discretization errors in inverse problems based on partial differential equation models. Multidimensional inverse problems are by nature computationally intensive, and a key challenge in practical applications is to reduce the computing time. In particular, a reduction by coarse discretization of the forward model is commonly used. Coarse discretization, however, introduces a numerical model discrepancy, which may become the predominant part of the noise, particularly when the data is collected with high accuracy. In the Bayesian framework, the discretization error has been addressed by treating it as a random variable and using the prior density of the unknown to estimate off-line its probability density, which is then used to modify the likelihood. In this article, the problem is revisited in the context of an iterative scheme similar to Ensemble Kalman Filtering (EnKF), in which the modeling error statistics is updated sequentially based on the current ensemble estimate of the unknown quantity. Hence, the algorithm learns about the modeling error while concomitantly updating the information about the unknown, leading to a reduction of the posterior variance.

Publication: Ph.D. thesis

Computational models are an essential tool to understand biological systems. A common challenge in this field is to find reduced models that offer a simpler effective description of a system with increased computational efficiency. Recent revived interest in applications of machine learning has produced algorithms that are naturally suited for this task. This thesis introduces dynamic Boltzmann distributions (DBDs) for model reduction of chemical reaction networks. DBDs are an unsupervised learning method, framed in the language of probabilistic graphical models. This allows a close connection to be made between DBDs and the description of chemical reaction networks by master equations. In this framework, this thesis shows how the physics of the system can be incorporated into otherwise application-agnostic machine learning algorithms. DBDs and their accompanying physics-informed machine learning algorithms provide a new path forward to apply reduced modeling methods to study reaction pathways at scale in synaptic neuroscience and other applications in biology.

Publication: Bachelor thesis

Inverse problems are by nature computationally intensive, and a key challenge in practical applications is to reduce the computing time without sacrificing the accuracy of the solution. When using Finite Element (FE) or Finite Difference (FD) methods, the computational burden of using a fine discretization is often unrealizable in practical applications. Conversely, coarse discretizations introduce a modeling error, which maybe become the predominant part of the noise, particularly when the data is collected with high accuracy. In the Bayesian framework for solving inverse problems, it is possible to attain a super-resolution in a coarse discretization by treating the modeling error as an unknown that is estimated as part of the inverse problem. It has been previously proposed to estimate the probability density of the modeling error in an off-line calculation that is performed prior to solving the inverse problem. In this thesis, a dynamic method to obtain these estimates is proposed, derived from the idea of Ensemble Kalman Filtering (EnKF). The modeling error statistics are updated sequentially based on the current ensemble estimate of the unknown quantity, and concomi- tantly these estimates update the likelihood function, reducing the variance of the posterior distribution. A small ensemble size allows for rapid convergence of the estimates, and the need for any prior calculations is eliminated. The viability of the method is demonstrated in application to Electrical Impedance Tomography (EIT), an imaging method that measures spatial variations in the conductivity distribution inside a body.

Publication: Bachelor thesis

The jet quenching effects of including recoil partons from interactions of high momentum partons with the QGP in Pb+Pb events are studied in the JEWEL Monte Carlo Event Generator. Momentum balance in the model shows that excluding recoil partons leads to a net momentum imbalance on the order of tens of GeV/c, indicating the necessity to include recoil partons in observables that depend on momentum conservation. When calculating the nuclear modification factor RAA, the generation of recoil hadrons that result from the hadronization of recoil partons requires a background subtraction procedure to be implemented due to the high number of recoil tracks as compared to benchmark p+p events. Furthermore, the non-uniform distribution of recoil tracks in pseudorapidity presents both a conceptual curiosity and exceptional challenges in sampling the recoil track background, in particular, choosing the region in the φ, η plane to sample for the density of jet transverse momentum. Several regions are compared for cone radii used in jet finding ranging from R = 0.2 to R = 0.5. We find that including recoil partons leads to a dependence of the nuclear modification factor on the cone radius that is not observed when recoil partons are excluded.