Grover’s quantum algorithm in Python

Breaking down the magic of quantum algorithms.

This project is based on what I learned from Chapter 15 of by Robert Geroch — Amazon.

Grover’s algorithm

Grover’s algorithm is used to invert a blackbox — given the output of some unknown blackbox, what was the input that generated it from a given set?

As an easy example, consider the problem of finding a needle in a haystack. Let the haystack consist of N integers from 0 to N-1, and the index of the needle be denoted by k_0. If we were to design a simple algorithm to solve this challenge, it would draw random numbers from the haystack, and check each time whether the chosen number is the needle. This requires N runs for 100% certainty.

The magic of Grover’s algorithm is that we can do better than that — in fact, we can do it O(sqrt(N)) steps! The quantum part enters by first rephrasing the problem in a probabilistic formulation: the goal is to find the needle with probability greater than 1–1/N. A detailed treatment is given in Geroch — only the relevant equations are given below. For a given guess k at the needle, define the operator V as:

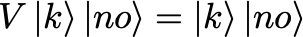
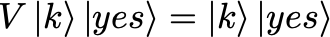
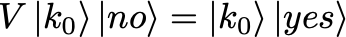
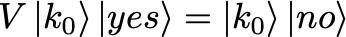
ie. for the state \ket{k} the output is unchanged, while the state \ket{k_0} causes the yes/no boolean to switch value.

As initial state, take:

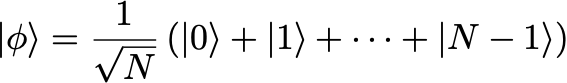
Define the yes/no state as

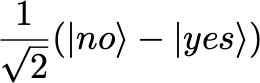
and the full input becomes

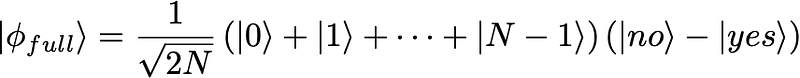
Furthermore, define the operator W as

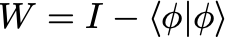
The algorithm then works by, at each step, applying the operators V and W to the current state, starting with

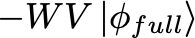
and then checking whether or not the probability has converged to a value greater than 1–1/N by taking the inner product with \bra{k_0}.

Classes

Let’s implement the algorithm in Python by defining some classes that represent the states and operations on those states. Note that in the code, no distinction is made between bra and ket states; rather, it is assumed that when operations are applied such as **<1|1> = 1**, it is done blindly but correctly.

First, we define the Basis_Vector class. A Basis_Vector is composed of a name and an index. The name identifies the state, e.g. |1> for integer 1, and the index identitifies an orthonormal set, that is, states of the same index are assumed to be orthonormal.

Second, we define the State_Pair class, which consists of a coefficient and a list of Basis_Vector. For example, 0.3 |2> |yes>has coefficient 0.3 and a list of Basis_Vector |2> |yes>, where the two elements of the list have names |2>and |yes>, respectively, and different orthonormal basis indices such as 1 and 2, respectively.

Third, we define a State class as a list of state pairs, which are assumed to be added to give the total state (coefficients of State_Pair may be negative for subtraction).

Some functions for adding and multiplying states have been defined as indicated. Note that subtraction is not supported; only negative coefficients for State_Pairs.

With these three classes we can now define any desired state, and perform simple manipulations such as addition and subtraction.

Operators

With little effort, operators V and W can now be defined to act on any desired state, as defined above:

Running the Code

Finally, we are ready to run the code. A length is chosen for the haystack of N=100, and some k_0 index for the needle (we’ll pretend we don’t know). The state corresponding to this needle is |k_0> and is implemented as:

which gives

Created k0 state: 1.000000000 |1>

Here, the name of the state is str(k0), and the index for the orthonormal set is chosen arbitrarily as 1. Next, the state |\phi> is generated as follows:

gives

Created phi state: 0.100000000 |0> + 0.100000000 |1> + 0.100000000 |2> + 0.100000000 |3> + ...

That is, a list pair_list of State_Pair is generated. Each State_Pair with coefficient 1/\sqrt{N}, and a list of Basis_Vector consisting of one elements. The one Basis_Vector has as name the integer from 0 to N-1 and as orthonormal index 1 (the same as k0). This state phi matches the expected:

Similarly, the yes/no state is generated, and the state phi_full is defined as the product of phi with the yes/no state:

gives:

Created yn state: -0.707106781 |yes> + 0.707106781 |no>

Finally, the state phi_full is:

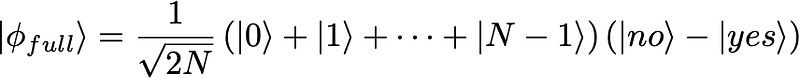
which is produced by:

giving:

Created phi full state: -0.070710678 |0> |yes> + 0.070710678 |0> |no> + -0.070710678 |1> |yes> + 0.070710678 |1> |no> + -0.070710678 |2> |yes> + 0.070710678 |2> |no> + -0.070710678 |3> |yes> + 0.070710678 |3> |no> + ...

Running the code now proceeds as follows. At each iteration, we apply the operators as mentioned previously:

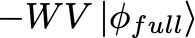
Next, we calculate the probability of observing k_0 by taking the inner product with the state \ket{k_0} (actually, we want the state \bra{k_0}, but as mentioned, we don’t make that distinction). We repeat this until the probability is greater than 1-1/N as desired, and print the result.

The code is:

giving:

-----------------------------------------------------

Probability of observing k0 for N = 100

-----------------------------------------------------

Step | Probability | Comparison with step number / N

-----------------------------------------------------

0000 | 0.010000000 | 0.010000

0001 | 0.087616000 | 0.020000

0002 | 0.230553626 | 0.030000

0003 | 0.416171557 | 0.040000

0004 | 0.615067914 | 0.050000

0005 | 0.795737513 | 0.060000

0006 | 0.929562290 | 0.070000

0007 | 0.995344400 | 0.080000

-----------------------------------------------------

Final step probability > 1-1/N = 0.990000

In only 8 (about sqrt(N=100)=10) steps, we have probability greater than 99% for finding the needle. The comparison is the basic random search algorithm, which has probability 8% after 8 steps. Pretty great!

The full test code can be found here.

Final thoughts

In this post we explored an algorithm that exposes the power of quantum algorithms. Further reference can be found in Chapter 15 of by Robert Geroch — Amazon.

Thanks for reading!