Two ways to do regression with neural networks

Neural network have so many hidden tricks. Here are some practical tips for using neural networks to do regression.

---

Regression vs. classification for practical purposes?

What is regression vs. classification? When it comes to practical neural networks, the difference is small: in regression tasks, the targets to be learned a continuous variables, rather than a discrete label representing a category. One-hot encoding is not the way to go here — in a regression task, the output of the network is often only a node.

The fact that the output should be continuous leads to two main ways to do regression:

1. Scale or whiten the targets during training, and then scale the outputs back with the same transformation in testing.
2. Let the last layer of the neural network be a linear layer (i.e. no activation function) such that the output can be continuous.

Let’s consider each one.

---

1. Scale the targets to be learned

It is common to scale the inputs to a neural network. To do a regression task, we could also scale the outputs such that they are not scattered Then, , you can scale the output back with the same transformation to get a continuous valued output.

For the scaling, you could scale the outputs of each neuron in the output layer to lie in the intervals[0,1] or [-1,1] . Even better is to whiten the outputs to have zero mean and unit variance, as is commonly done for the inputs.

The downside of this approach is that you need can introduce extra error during testing from the scaling, since the training did not try to reproduce the actual continuous valued outputs directly. If your target regression values to be learned need to be highly precise, this can be a problem.

A second problem is that your outputs for the regression task may not be simply uniform or Gaussian distributed — you may have something which looks bimodal, or otherwise has some large outliers. If the distribution is bimodal, your whitening transformation would push the targets to be learned away from zero, making the task harder. If the distribution has large outliers, these would still be large outliers after the transformation and would probably not be fit well.

A strategy to overcome this is to look inspect your data for correlations between input and outputs. For example, you may identify that the two peaks of the target bimodal distribution correspond to two different regimes of the input data. In this case, you should consider training two networks — one for each regime of inputs.

---

1. Let the last layer of the neural network be a linear layer

The common equation for a the output from a layer given previous layer x and weight matrix W and bias b is:

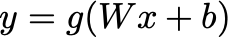
where g is the activation function (ReLU, leaky ReLU, tanh or otherwise sigmoid). Some activation functions such as ReLU give only positive outputs; others such as tanh produce outputs in an open set (-1,1) . Whichever the case, this is not good for a regression task.

A linear layer is instead just:

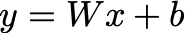
Clearly, this can produce any real valued output. A simple trick to do regression with neural networks then is to justlet the output layer be a linear layer.

This seems like a simpler solution than the first method at first, but it has it’s own challenges. If you need to learn real valued targets, this will require large values for weight and bias parameters. Unfortunately, especially if you are using normalization for the input layer, or even batch normalization between the layers, the weights and biases in most other layers will be around 0 (approximately in -1,1).

The learning rates for the final liner layer therefore have to be chosen independently of the learning rates for the other layers. Otherwise, you will either not get the linear layer to learn if the learning rate is too low (resulting in poor accuracy), or the learning rate for the other layers will be so high that the learning will be unstable and will not settle in a nice minimum.

Final thoughts

It’s not clear there’s a real winner here. Extra learning rates introduce more hyper-parameters, and tuning those is just an absolute joy. But scaling the output layer can be tricky if you the distribution of target values isn’t simple.

As with so many other topics in machine learning, probably the best advice is: try both and see what sticks!

You may be curious: couldn’t you just use the first method (scale the targets to be learned), but then the scaling as part of the learning problem? However, this is futile, as it is equivalent to adding a linear layer as in the last layer as in the second method and learning the weight matrix and bias vector which are then the scale and shift parameters. You would therefore again likely need separate learning rates for the output layers.